DSQNet: A Deformable Model-Based Supervised Learning Algorithm for Grasping Unknown Occluded Objects

Our recognition-based grasping method proceeds in three steps as shown in the below figure: (i) a trained segmentation network is used to segment a partially observed point cloud into a set of simpler point clouds; (ii) The trained DSQNet converts each point cloud into a deformable superquadric primitive, with its collective union representing the full object shape; (iii) grasp poses are generated in a gripper-dependent manner from the recognized full shapes.

Superquadrics are an extended set of quadric surfaces that can be used to represent diverse shapes ranging from boxes, cylinders, and ellipsoids to bi-cones, octahedra, and other complex symmetric shapes, even those with rounded corners and edges. Superquadrics are further categorized into superellipsoids, superhyperboloids, and supertoroids; for our modeling purposes the superellipsoids are sufficient. The corresponding implicit equations for a superquadric surface with size parameters \((a_1, a_2, a_3) \in \mathbb{R}_+^3\) and shape parameters \((e_1, e_2) \in \mathbb{R}_+^2\) are of the form: for \(\textbf{x} = (x, y, z)\), $$ \begin{equation*} f(\textbf{x})=\left(\left|\frac{x}{a_1}\right|^{\frac{2}{e_2}} + \left|\frac{y}{a_2}\right|^{\frac{2}{e_2}}\right)^{\frac{e_2}{e_1}} + \left|\frac{z}{a_3}\right|^{\frac{2}{e_1}} = 1. \end{equation*} $$ Although more expressive than quadrics, superquadrics are still limited by their inability to capture tapered and bent objects. Deformable superquadrics are obtained by applying global tapering and bending deformations as shown below.

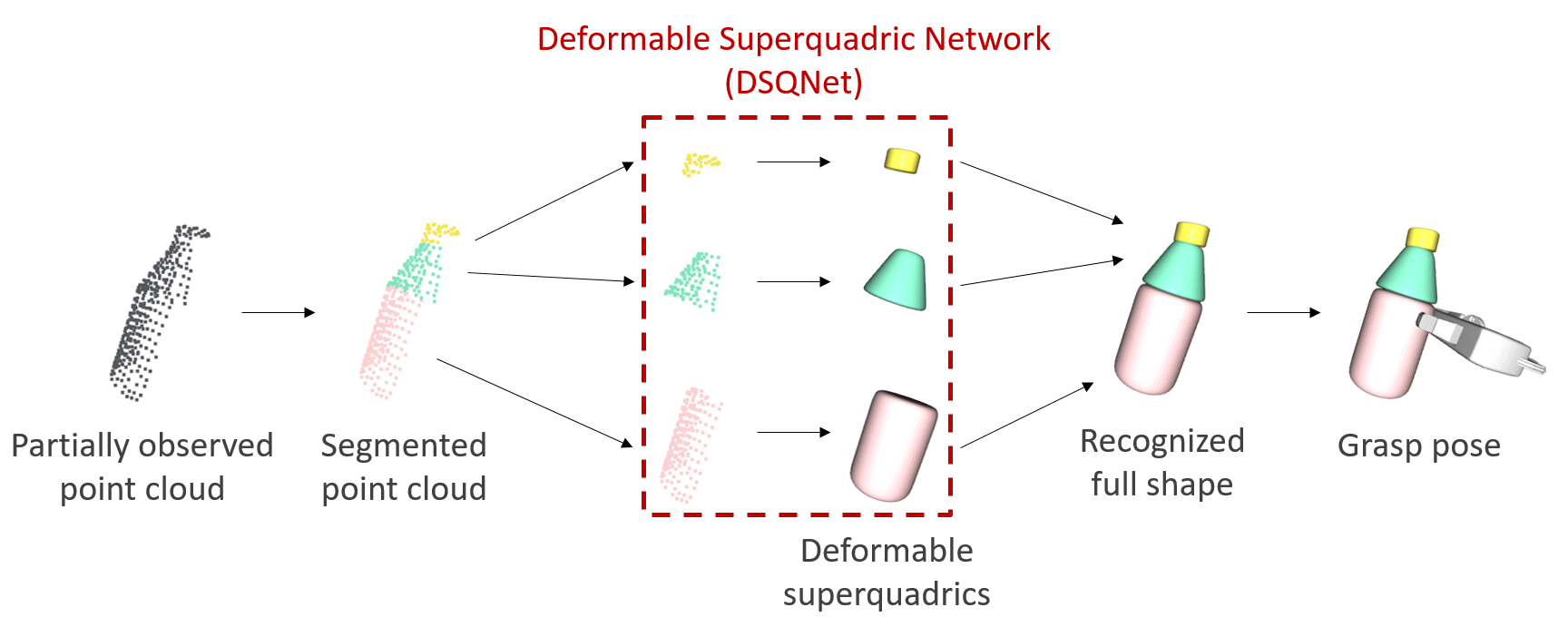
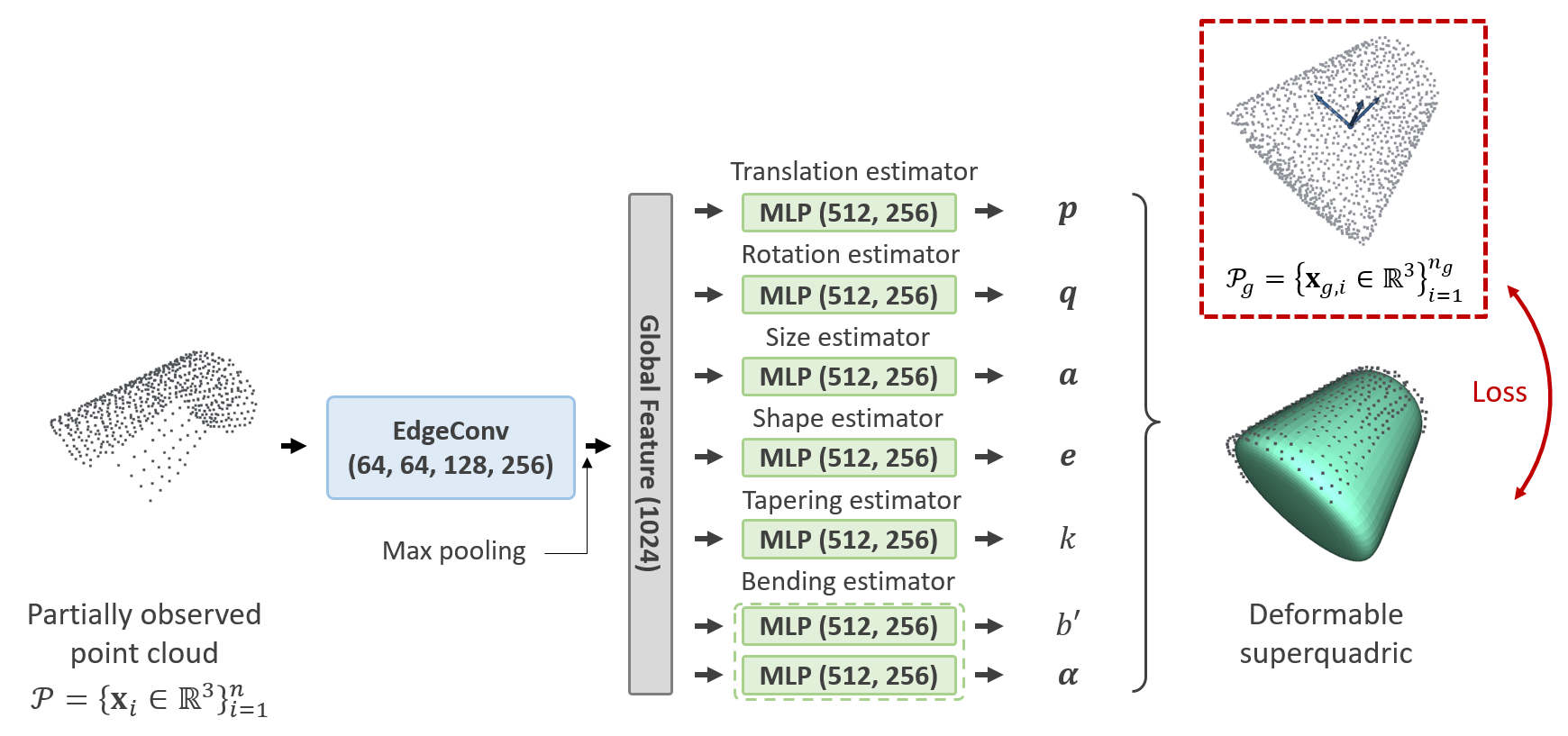
We design a neural network architecture, referred to as the Deformable Superquadric Network (DSQNet), which takes partially observed point cloud data as input and outputs the eight parameters and the pose of the deformable superquadric. This output aims to reconstruct the full shape of the object, including its occluded parts. The network is trained to minimize fitting errors between the ground-truth point cloud and the predicted deformable superquadric.

Recognition is achieved quickly and accurately with a simple forward pass through the neural network. Extensive experiments and benchmark comparisons using a variety of everyday objects demonstrate both the strengths of our approach and potential areas for improvement. For recognizing household objects, our method achieves the highest accuracy (in terms of volumetric IoU) and the fastest computation speeds among existing recognition-based methods.

Once the shape of an object is recognized as a set of deformable superquadric primitives, conventional grasp pose generation techniques can be applied for a given gripper. In this paper, we focus on parallel jaw grippers and adopt an antipodal points sampling-based grasp pose generation method. We first develop an efficient algorithm for sampling antipodal points on deformable superquadric primitives, followed by a grasp pose generation algorithm that utilizes the sampled pairs of antipodal points.

We have additionally developed a shape uncertainty-aware grasping algorithm to assist in grasp pose planning and enhance grasp performance in more challenging scenarios. While DSQNet achieves the best recognition performance on both synthetic and real-world objects, perfect shape recognition is not always feasible. If the generated grasp pose targets an erroneous part of the recognized shape, the gripper may fail to grasp the object. To mitigate the risk of grasping incorrect parts, we introduce a new grasp score that accounts for shape uncertainty.